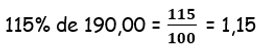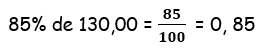Teremos aqui um desempenho mais alto para o ano letivo.
Bem-vindo a Página de [AIM].
Abaixo estão as Ajudas Iniciais em Matemática:
Matemática 3° Bimestre
Relações Trigonométricas no Triângulo Retângulo:

Hipotenusa, Cateto Oposto e Cateto Adjacente:
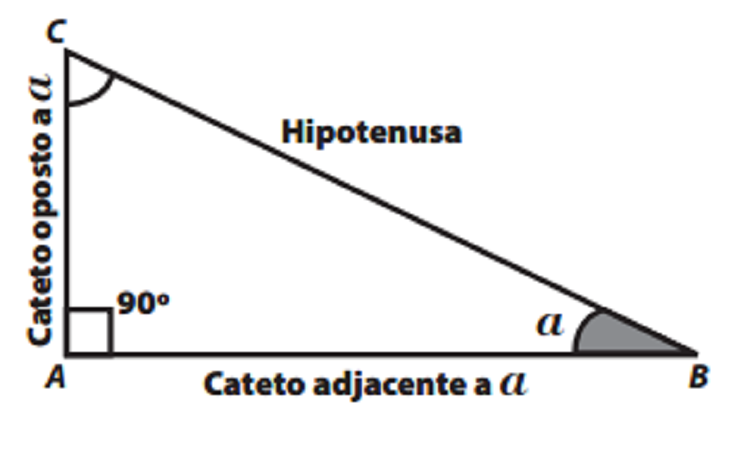
Em um triângulo retângulo, a HIPOTENUSA é o maior lado, o CATETO OPOSTO é aquele em frente a um determinado ângulo e um CATETO ADJACENTE é aquele ao lado de um determinado ângulo.
Nós usamos palavras especiais para descrever os lados dos triângulos retângulos.
A hipotenusa de um triângulo retângulo é sempre o lado oposto ao ângulo reto. Ela é o maior lado do triângulo retângulo.
Os outros dois lados são chamados cateto oposto e cateto adjacente. Esses lados são definidos em relação a um ângulo.
O cateto oposto fica em frente a um determinado ângulo.
O cateto adjacente é aquele que fica ao lado de um determinado ângulo, mas não é a hipotenusa.
Ao unirmos todas as informações acima, da perspectiva do ângulo  temos:
Por que essas palavras são importantes?
Estamos prestes a aprender as funções trigonométricas — seno, cosseno e tangente — que são definidas por meio das palavras hipotenusa, cateto oposto e cateto adjacente.
Agora que já sabemos o que é hipotenusa, cateto oposto e cateto adjacente vamos adiante.
Seno, Cosseno e Tangente:
Seno pode ser representado por Sen
*O Seno é igual ao cateto oposto dividido pela hipotenusa.
Assim: Sen=
Cosseno pode ser representado por Cos
*O cosseno é igual ao cateto adjacente dividido pela hipotenusa.
Assim: Cos=
Tangente pode ser representado por Tan
*A Tangente é igual ao cateto oposto dividido pelo cateto adjacente.
Assim: Tan=







Matemática 4° Bimestre
Matemática Financeira - Porcentagem:


Porcentagem:
É frequente o uso de expressões que refletem acréscimos ou reduções em preços, números ou quantidades, sempre tomando por base 100 unidades.
Alguns exemplos:
-
A gasolina teve um aumento de 15%.
Significa que em cada R$100 houve um acréscimo de R$15,00.
-
O cliente recebeu um desconto de 10% em todas as mercadorias.
Significa que em cada R$100 foi dado um desconto de R$10,00.
-
Dos jogadores que jogam no Grêmio, 90% são craques.
Significa que em cada 100 jogadores que jogam no Grêmio, 90 são craques.
Considere o seguinte problema:
João vendeu 50% dos seus 50 cavalos. Quantos cavalos ele vendeu?
Para solucionar esse problema, devemos aplicar a taxa percentual (50%) sobre o total de cavalos.
50% de 50 = .50 = 25 cavalos.
Logo, ele vendeu 25 cavalos, que representa a porcentagem procurada. Portanto, chegamos à seguinte definição:
Porcentagem é o valor obtido ao aplicarmos uma taxa percentual a um determinado valor.
Exemplos:
Acréscimo:
É muito comum, ao comprarmos um produto em uma loja, vermos que o valor de seu preço à vista sofre um aumento (acréscimo), caso o seu pagamento seja realizado a prazo.
Vamos analisar os exemplos a seguir e encontrar as suas soluções.
Exemplos:
1 - A loja Havan oferece ótimos preços nas compras à vista de todos os seus produtos. Porém, na compra de uma calça masculina, que custa R$ 190,00, por exemplo, caso o pagamento seja realizado em prestações (a prazo), seu valor sofrerá um acréscimo de 15%. Quanto custará essa calça pagando a prazo?
Como Resolver:
R$ 190,00 corresponde a 100%. Como o acréscimo será de 15% devemos somar (+) as duas porcentagens.
100% + 15% = 115%
Agora, vamos calcular 115% de R$ 190,00 para encontrar o valor procurado.
1,15.190 = 218,5 (valor a pagar)
218,5 - 190 = 28,5 (valor do acréscimo)
Ou seja, a calça custará R$ 218,50, caso seu pagamento seja realizado a prazo.
2 - Uma empresa de distribuição de energia elétrica, cobra pela ativação da rede elétrica residencial, uma taxa de R$ 200,00. Para o próximo mês, essa empresa anunciou um aumento de 5% sobre a taxa atual. Qual será a taxa de ativação de rede após o acréscimo anunciado?
Como Resolver:
R$ 200,00 corresponde a 100%. Como o acréscimo será de 5% devemos somar as duas porcentagens.
100% + 5% = 105%
Agora, vamos calcular 105% de R$ 200,00 para encontrar o valor procurado.
1,05.200 = 210 (valor a pagar)
10,00 (valor do acréscimo)
Sendo assim, no próximo mês, a taxa de ativação de rede desta empresa será R$ 210,00.
3 - Pedro paga mensalmente R$ 480,00 pelo aluguel da casa onde mora. O proprietário da casa anunciou um aumento de 10% sobre o valor do aluguel para o mês seguinte. Quanto Pedro pagará pelo aluguel após o acréscimo previsto?
Como Resolver:
R$ 480,00 corresponde a 100%. Como o acréscimo será de 10% devemos somar as duas porcentagens.
100% + 10% = 110%
Agora, vamos calcular 110% de R$ 480,00 para encontrar o valor acrescido.
1,1.480 = 528 (valor a pagar)
528 – 140 = 48 (valor do acréscimo)
Desta forma, encontramos R$ 528,00 como valor a ser pago por Pedro após o acréscimo que será feito pelo proprietário da residência.
Desconto:
São muitas as situações diárias nas quais podemos observar as aplicações de descontos. Nas lojas, nos bancos ou no comércio em geral, esse conhecimento é importante, útil e indispensável ao diálogo entre atendentes e clientes envolvidos numa transação financeira.
Ao comprarmos um produto e pagá-lo à vista, geralmente obteremos um desconto.
Essa frase ilustra umas das muitas possibilidades de ocorrência de descontos financeiros. Em seguida, apresentarei alguns exemplos e suas respectivas soluções, assim, você poderá analisá-las e chegar à compreensão do problema gerador desta Ajuda Inicial [AI].
Exemplos:
1 - Numa loja, uma camisa custa R$ 130,00. Caso seu pagamento seja realizado à vista, haverá um desconto de 15%. Nessas circunstâncias, qual será o valor pago pela camisa, caso o cliente resolva efetuar o pagamento à vista?
Como Resolver:
R$ 130,00 corresponde a 100%. Como o desconto será de 15% devemos subtrair (-) a segunda porcentagem da primeira.
100% - 15% = 85%
Agora, vamos calcular 85% de R$ 130,00 para encontrar o valor procurado.
0,85.130 = 110,5 (valor a pagar)
130 – 110,5 = 19, 5 (valor do desconto)
Ao pagar a camisa à vista o cliente obteve um desconto de R$ 19,50, pagando apenas R$ 110,50 por ela.
2 - Em uma promoção, certa loja ofereceu desconto de 35% na compra de um par de tênis. Qual o valor pago pelo par de tênis nessa promoção, sabendo que sem o desconto ele custa R$ 132,00?
Como Resolver:
R$ 132,00 corresponde a 100%. Como o desconto será de 35%, subtrairemos a segunda porcentagem da primeira.
100% - 35% = 65%
Agora, vamos calcular 65% de R$ 132,00 e encontrar o valor procurado.
0,65.132 = 85,8 (valor a pagar)
132 – 85,8 = 46,2 (valor do desconto)
Ao pagar o par de tênis à vista o cliente obteve um desconto de R$ 46,20, pagando apenas R$ 85,80 por eles.
3 - Após anos de espera e de economias, Júlio e Marta realizarão o sonho da casa própria. A casa dos seus sonhos custa R$ 190 000,00, mas à vista eles ganharão um desconto de 12%. Sabendo que as economias de Júlio e Marta são suficientes para efetuar essa compra à vista, quanto eles pagarão por esta casa?
Como Resolver:
R$ 190 000,00 corresponde a 100%. Como o desconto será de 12%, subtrairemos a segunda porcentagem da primeira.
100% - 12% = 88%
Agora, basta calcular 88% de R$ 190 000,00 e encontrar o valor procurado.
0,88.190 000 = 167 200 (valor a pagar)
190.000 – 167.200 = 22 800 (valor do desconto)
Ao comprar essa casa à vista o casal economizará R$ 22 800,00, pagando apenas R$ 167 200,00 pelo imóvel.